Matrix Functions
The Movie Toolbox provides a number of functions that allow you to work with transformation matrices. This section describes those functions. For more information about transformation matrices, see
"The Transformation Matrix"
. For descriptions of fixed-point and fixed-rectangle structures, see
"The Fixed-Point and Fixed-Rectangle Structures"
.
Note
The functions described in this section do not appear in the MPW interface file
Movies.h
; rather, they appear in the
ImageCompression.h
interface file.
SetIdentityMatrix
The
SetIdentityMatrix
function allows your application to set the contents of a matrix so that it performs no transformation. Such matrices are referred to as
identity matrices.
pascal void SetIdentityMatrix (MatrixRecord *matrix);
-
matrix
-
Contains a pointer to a matrix structure. The
SetIdentityMatrix
function updates the contents of this matrix so that the matrix describes the identity matrix.
GetMatrixType
The
GetMatrixType
function allows your application to obtain information about a matrix. This information indicates the nature of the transformation defined by the matrix.
pascal short GetMatrixType (const MatrixRecord *m);
-
m
-
Points to the matrix for this operation.
DESCRIPTION
The
GetMatrixType
function returns an integer that indicates the nature of the transformation defined by the matrix. The following values are possible:
-
identityMatrixType
-
Indicates that the specified matrix is an identity matrix.
-
translateMatrixType
-
Indicates that the specified matrix defines a translation operation.
-
scaleMatrixType
-
Indicates that the specified matrix defines a scaling operation.
-
scaleTranslateMatrixType
-
Indicates that the specified matrix defines both a translation operation and a scaling operation.
-
linearMatrixType
-
Indicates that the specified matrix defines a rotation, skew, or shear operation.
-
linearTranslateMatrixType
-
Indicates that the specified matrix defines both a translation operation and a rotation, skew, or shear operation.
-
perspectiveMatrixType
-
Indicates that the specified matrix defines a perspective (nonlinear) operation.
CopyMatrix
The
CopyMatrix
function copies the contents of one matrix into another matrix.
pascal void CopyMatrix (const MatrixRecord *m1, MatrixRecord *m2);
-
m1
-
Specifies the source matrix for the copy operation.
-
m2
-
Contains a pointer to the destination matrix for the copy operation. The
CopyMatrix
function copies the values from the matrix specified by the
m1
parameter into this matrix.
DESCRIPTION
The
CopyMatrix
function is a convenience function for copying the contents of one matrix to another. You can achieve the same results by using the Memory Manager's
BlockMove
routine, or by assigning the contents of one matrix record to another directly.
EqualMatrix
The
EqualMatrix
function compares two matrices and returns a result that indicates whether the matrices are equal.
pascal Boolean EqualMatrix (const MatrixRecord *m1,
const MatrixRecord *m2);
-
m1
-
Contains a pointer to one matrix for the compare operation.
-
m2
-
Contains a pointer to the other matrix for the compare operation.
DESCRIPTION
The
EqualMatrix
function returns a Boolean value that indicates whether the specified matrices are equal. If the matrices are equal, the function sets this returned value to
true
. Otherwise, it sets the returned value to
false
.
TranslateMatrix
The
TranslateMatrix
function allows your application to add a translation value to a specified matrix.
pascal void TranslateMatrix (MatrixRecord *m,
Fixed deltaH, Fixed deltaV);
-
m
-
Contains a pointer to the matrix structure for this operation.
-
deltaH
-
Specifies the value to be added to the x coordinate translation value.
-
deltaV
-
Specifies the value to be added to the y coordinate translation value.
ScaleMatrix
The
ScaleMatrix
function allows your application to modify the contents of a matrix so that it defines a scaling operation.
pascal void ScaleMatrix (MatrixRecord *m, Fixed scaleX,
Fixed scaleY, Fixed aboutX, Fixed aboutY);
-
m
-
Contains a pointer to a matrix structure. The
ScaleMatrix
function updates the contents of this matrix so that the matrix describes a scaling operation--that is, it concatenates the respective transformations onto whatever was initially in the matrix structure. You specify the magnitude of the scaling operation with the
scaleX
and
scaleY
parameters. You specify the anchor point with the
aboutX
and
aboutY
parameters.
-
scaleX
-
Specifies the scaling factor applied to x coordinates.
-
scaleY
-
Specifies the scaling factor applied to y coordinates.
-
aboutX
-
Specifies the x coordinate of the anchor point.
-
aboutY
-
Specifies the y coordinate of the anchor point.
RotateMatrix
The
RotateMatrix
function allows your application to modify the contents of a matrix so that it defines a rotation operation.
pascal void RotateMatrix (MatrixRecord *m, Fixed degrees,
Fixed aboutX, Fixed aboutY);
-
m
-
Contains a pointer to a matrix structure. The
RotateMatrix
function updates the contents of this matrix so that the matrix describes a rotation operation--that is, it concatenates the rotation transformations onto whatever was initially in the matrix structure. You specify the direction and amount of rotation with the
degrees
parameter. You specify the point of rotation with the
aboutX
and
aboutY
parameters.
-
degrees
-
Specifies the number of degrees of rotation.
-
aboutX
-
Specifies the x coordinate of the anchor point of rotation.
-
aboutY
-
Specifies the y coordinate of the anchor point of rotation.
SkewMatrix
The
SkewMatrix
function allows your application to modify the contents of a matrix so that it defines a skew transformation. A skew operation alters the display of an element along one dimension--for example, converting a rectangle into a parallelogram is a skew operation.
pascal void SkewMatrix (MatrixRecord *m, Fixed skewX, Fixed skewY,
Fixed aboutX, Fixed aboutY);
-
m
-
Contains a pointer to the matrix for this operation. The
SkewMatrix
function updates the contents of this matrix so that it defines a skew operation--that is, it concatenates the respective transformations onto whatever was initially in the matrix structure. You specify the magnitude and direction of the skew operation with the
skewX
and
skewY
parameters. You specify an anchor point with the
aboutX
and
aboutY
parameters.
-
skewX
-
Specifies the skew value to be applied to x coordinates.
-
skewY
-
Specifies the skew value to be applied to y coordinates.
-
aboutX
-
Specifies the x coordinate of the anchor point.
-
aboutY
-
Specifies the y coordinate of the anchor point.
ConcatMatrix
The
ConcatMatrix
function concatenates two matrices, combining the transformations described by both matrices into a single matrix.
pascal void ConcatMatrix (const MatrixRecord *a, MatrixRecord *b);
-
a
-
Contains a pointer to the source matrix.
-
b
-
Contains a pointer to the destination matrix. The
ConcatMatrix
function performs a matrix multiplication operation, combining the two matrices, and leaves the result in the matrix specified by this parameter.
DESCRIPTION
The form of the operation that the
ConcatMatrix
function performs is shown by the following formula:
[B] = [B] x [A]
This is a matrix multiplication operation. Note that matrix multiplication is not commutative.
InverseMatrix
The
InverseMatrix
function creates a new matrix that is the inverse of a specified matrix.
pascal Boolean InverseMatrix (const MatrixRecord *m,
MatrixRecord *im);
-
m
-
Contains a pointer to the source matrix for the operation.
-
im
-
Contains a pointer to a matrix structure that is to receive the new matrix. The
InverseMatrix
function updates this structure so that it contains a matrix that is the inverse of that specified by the
m
parameter.
DESCRIPTION
The
InverseMatrix
function returns a Boolean value that indicates whether it could create an inverse matrix. If the function could create an inverse matrix, it sets this returned value to
true
. Otherwise, the function sets the returned value to
false
.
TransformPoints
The
TransformPoints
function allows your application to transform a set of QuickDraw points through a specified matrix.
pascal OSErr TransformPoints (const MatrixRecord *mp, Point *pt1,
long count);
-
mp
-
Contains a pointer to the transformation matrix for this operation.
-
pt1
-
Contains a pointer to the first QuickDraw point to be transformed.
-
count
-
Specifies the number of QuickDraw points to be transformed. These points must be stored immediately following the point specified by the
pt1
parameter.
SEE ALSO
You can transform a set of QuickDraw points that are made up of fixed values by calling the
TransformFixedPoints
function, which is described in the next section.
TransformFixedPoints
The
TransformFixedPoints
function allows your application to transform a set of fixed points through a specified matrix.
pascal OSErr TransformFixedPoints (const MatrixRecord *m,
FixedPoint *fpt, long count);
-
m
-
Contains a pointer to the transformation matrix for this operation.
-
fpt
-
Contains a pointer to the first fixed point to be transformed.
-
count
-
Specifies the number of fixed points to be transformed. These points must be stored immediately following the point specified by the
fpt
parameter.
SEE ALSO
You can transform a set of fixed points that is made up of short integer values by calling the
TransformPoints
function, which is described in the previous section.
TransformRect
The
TransformRect
function allows your application to transform the upper-left and lower-right points of a rectangle through a specified matrix.
pascal Boolean TransformRect (const MatrixRecordPtr m, Rect *r,
FixedPoint *fpp);
-
m
-
Specifies the matrix for this operation.
-
r
-
Contains a pointer to the structure that defines the rectangle to be transformed. The
TransformRect
function returns the updated coordinates into the structure referred to by this parameter. If the resulting rectangle has been rotated or skewed (that is, the transformation involves operations other than scaling and translation), the function sets the returned Boolean value to
false
and returns the coordinates of the rectangle that encloses the transformed rectangle. The function then updates the points specified by the
fpp
parameter to contain the coordinates of the four corners of the transformed rectangle.
-
fpp
-
Contains a pointer to an array of four fixed points. The
TransformRect
function returns the coordinates of the four corners of the rectangle after the transformation operation.
-
If you do not want this information, set this parameter to
nil
.
DESCRIPTION
The
TransformRect
function returns a Boolean value indicating the nature of the result rectangle. If the matrix defines transformations other than translation and scaling, the
TransformRect
function sets the returned value to
false
, updates the rectangle specified by the
r
parameter to define the boundary box of the resulting rectangle, and places the coordinates of the corners of the resulting rectangle in the points specified by the
fpp
parameter. If the transformed rectangle and its boundary box are the same, the function sets the returned value to
true
.
TransformFixedRect
The
TransformFixedRect
function allows your application to transform the upper-left and lower-right points of a rectangle through a specified matrix. This rectangle must be specified by fixed points.
pascal Boolean TransformFixedRect (MatrixRecord *m,
FixedRect *fr,
FixedPoint *fpp);
-
m
-
Contains a pointer to the matrix for this operation.
-
fr
-
Contains a pointer to the structure that defines the rectangle to be transformed. The
TransformFixedRect
function returns the updated coordinates into the structure referred to by this parameter. If the resulting rectangle has been rotated or skewed (that is, the transformation involves operations other than scaling and translation), the function sets the returned Boolean value to
false
and returns the coordinates of the boundary box of the transformed rectangle. The function then updates the points specified by the
fpp
parameter to contain the coordinates of the four corners of the transformed rectangle.
-
fpp
-
Contains a pointer to an array of four fixed points. The
TransformFixedRect
function returns the coordinates of the four corners of the rectangle after the transformation operation.
-
If you do not want this information, set this parameter to
nil
.
DESCRIPTION
The
TransformFixedRect
function returns a Boolean value indicating the nature of the result rectangle. If the matrix defines transformations other than translation and scaling, the
TransformFixedRect
function sets the returned value to
false
, updates the rectangle specified by the
fr
parameter to define the boundary box of the resulting rectangle, and places the coordinates of the corners of the resulting rectangle in the points specified by the
fpp
parameter. If the transformed rectangle and its boundary box are the same, the function sets the returned value to
true
.
SEE ALSO
You can transform a standard rectangle by calling the
TransformRect
function, which is described in the previous section.
TransformRgn
The
TransformRgn
function allows your application to apply a specified matrix to a region.
pascal OSErr TransformRgn (MatrixRecordPtr matrix, RgnHandle r);
-
matrix
-
Points to the matrix for this operation. The
TransformRgn
function currently supports only translating and scaling operations.
-
r
-
Specifies the region to be transformed. The
TransformRgn
function transforms each point in the region according to the contents of the specified matrix.
ERROR CODES
Memory Manager errors
RectMatrix
The
RectMatrix
function allows your application to create a matrix that performs a translate and scale operation as described by the relationship between two rectangles.
pascal void RectMatrix (MatrixRecord *matrix, const Rect *srcRect,
const Rect *dstRect);
-
matrix
-
Contains a pointer to a matrix structure. The
RectMatrix
function updates the contents of this matrix so that the matrix describes a transformation from points in the rectangle specified by the
srcRect
parameter to points in the rectangle specified by the
dstRect
parameter. The previous contents of the matrix are ignored.
-
srcRect
-
Contains a pointer to the source rectangle.
-
dstRect
-
Contains a pointer to the destination rectangle.
DESCRIPTION
You specify the two rectangles; the function returns the appropriate matrix.
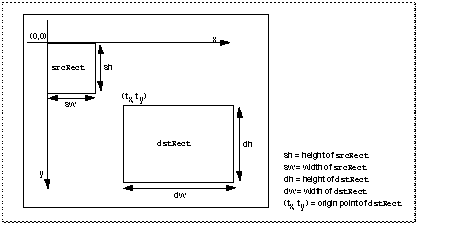
Figure 43
shows how this matrix transforms the source image.
Figure 43
Transforming an image with the
RectMatrix
function
Calling the
RectMatrix
function with the two rectangles shown in
Figure 43
results in the matrix shown in
Figure 44
.
Figure 44
Matrix created as a result of calling the
RectMatrix
function
SEE ALSO
If you call the
TransformRect
function (described on
TransformRect
) and supply the matrix produced by the
RectMatrix
function along with the source rectangle you specified when you called the
RectMatrix
function, the result is equivalent to the destination rectangle you specified.
MapMatrix
The
MapMatrix
function alters an existing matrix so that it defines a transformation from one rectangle to another, similar to the
MapRect
and
MapRegion
routines that are described in
Inside Macintosh: Imaging.
pascal void MapMatrix (MatrixRecord *matrix, Rect *fromRect,
Rect *toRect);
-
matrix
-
Contains a pointer to a matrix structure. The
MapMatrix
function modifies this matrix so that it performs a transformation in the rectangle specified by the
toRect
parameter that is analogous to the transformation it currently performs in the rectangle specified by the
fromRect
parameter.
-
fromRect
-
Contains a pointer to the source rectangle.
-
toRect
-
Contains a pointer to the destination rectangle.
DESCRIPTION
The
MapMatrix
function affects only the scaling and translation attributes of the matrix. This function is similar to
RectMatrix
, with the exception that
MapMatrix
concatenates the translation and scaling operations to the previous contents of the matrix, whereas
RectMatrix
first sets the matrix to the identity state.
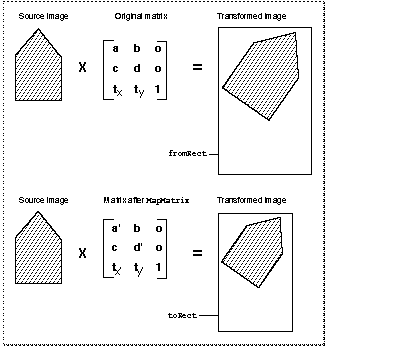
Figure 45
shows how the matrix that you obtain from the
MapMatrix
function transforms a source image.
Figure 45
Transforming an image with the
MapMatrix
function
SEE ALSO
You can create a matrix that maps one rectangle to another by calling the
RectMatrix
function, which is described in the previous section.
© 1999 Apple Computer, Inc.Previous | Overview | Contents | Next